Visual & Media Studies Academic Journal
ISSN 2299-906X
2. GEOMETRIES OF CYBERSPACE
When geometrizing, man creates and defines the spatial coordinates, which provide him with basic orientation in the surrounding world. First, he tries to capture spatial relationships, and only then, says Norberg-Schulz, geometric patterns may appear.
The world can be organized around sets of central points, broken into named regions, or linked with memorized paths. [1]
Geometries visualize mathematical rigor. But in cyberspace, they do not occur in the same forms as in the physical world. Geometric systems in cyberspace do not fulfill their mathematical measuring and descriptive tasks, but they occur in the cyberspace in various forms that can be described as geometric metaphors.
2.1. Geometric visualizations and metaphors
In cyberspace there is no scale or reference point, therefore all measuring and descriptive activities, for which geometries are created, are meaningless. So why do we need geometries in cyberspace if their principal task is to measure and describe spatial coordinates which cannot be implemented?
The answer to this question should be sought by moving away from perceiving geometry only in terms of cold mathematical structures or scientific methods. Peg Rawers, in her publication Space, Geometry and Aesthetics; through Kant and towards Deleuze proves that the phenomenon of geometry is that geometry is not only a mathematical method for constructing and describing space, but also is an aesthetic procedure, questioning the beliefs that are focused only on scientific forms of knowledge. Geometric figures, according to Rawers, can also be understood as an aesthetic expression of geometric thinking. The aesthetic geometry thus becomes a temporary, technical improvement of memory (e.g., intuition), and part of the mind space.
Birth of aesthetics based on the new geometry is a long process and it depends on the degree of absorption of scientific theories in the culture:
Geometric thinking may therefore be composed of dynamic embodiments, reconfiguring the relationship between aesthetics, space and the sensing subject. As a result, new ‘figure-subjects’ are opened up through which geometry may also enable cross-disciplinary examinations; especially for ontological research in philosophy, architectural design, art history and spatial practices in the visual arts. [2]
For Kant, various mental models generate the experience of geometry: pure intuition, sense-intuitions, technical and aesthetic activities.
“In metaphysical philosophy, geometry is also frequently taken to be an exemplary form of pure intuition and abstract ideas, thereby confirming the existence of pure, but inaccessible, transcendental knowledge” [3].
Rawers emphasizes that the dynamic relationship between space, geometry and aesthetics can be very productive for contemporary artists, especially for those studying alternative spaces in which the geometry can be understood without restrictions imposed by its scientific form accompanying the creation of “real” prerogatives. Therefore, the existing systems of geometry should be examined in terms of their “usefulness” for the creation of cyberspace.
2.2. Euclidean geometry in cyberspace
Of all geometric systems, Euclidean geometry is the oldest and most deeply rooted in the popular consciousness. Although it has long been proven that we live in curved, non-Euclidean space, we continue to build the space of everyday life in accordance to the Euclid’s postulates. This is primarily because Euclidean geometry is the most convenient existing geometric system. Poincaré says:
Just as it makes no sense to ask if the metric system is true and the old system measurement are false, or if Cartesian coordinates are true and polar ones false. One geometry cannot be more true than another; it can only be more convenient. Euclidean geometry is, and will remain, the most convenient. [4]
Another reason for using it is the fact that non-Euclidean geometry is almost unconceivable from the human scale perspective, which makes the Euclidean forms a much better choice in describing human’s space. In hyperbolic space, Euclidean form is approachable but not attainable.
Euclid’s Elements had a tremendous influence on Western culture. It formed a basic component of the standard intellectual education:
First, there is a sense of certainty – that a world full of irrational beliefs and shaky speculations, the statements found in the Elements were proven true beyond a shadow of a doubt. And although certain features in both the assumptions and methods of reasoning used by Euclid have been questioned over the centuries, the astonishing fact is that after two thousand years, no one has ever found an actual “mistake” in The Elements – that is to say a statement that did not follow logically from the assumptions. [5]
Since the Euclidean geometry is used to create and describe the existential space, it is clear that virtual worlds are also constructed in accordance to its rules. More precisely, according to the principles of geometrical metaphors of forms, relations and representations based on Euclidean geometry. Constructing virtual worlds on the foundations of Euclidean geometry is a part of the process of importing known elements into the new, unknown environment. It is an attempt to equip this new environment with human dimension and is part of a settlement process. It is also, as in the physical world, an attempt to give deeper meaning to the man’s existence, his proportions and the matrix of the universe.
Matters of convenience and continuity between the virtual and the real world are important factors standing behind the formation of the new environment. Michael Benedikt, when describing his idea for the architectural development of cyberspace, argues for "importing" useful laws of physics to the environment of cyberspace. He justifies it as allowing for a better orientation and accessibility of data. However, he proposes to conduct this process on a selective basis, because, as he says, not all the features of the physical world are suitable for the simulation in cyber worlds.
In metaphysical philosophy, geometry is also frequently taken to be an exemplary form of pure intuition and abstract ideas, thereby confirming the existance of pure, but inaccessible, transcendental knowledge. (Rawers)
The fact that non-Euclidean spaces can function independently in two-dimensional space opens a window to a whole new understanding of space. In fact, it is a revolution in thinking about space and it has changed the concept of space forever. Instead of a three-dimensional filled with objects and surrounding us space (structure), we can perceive the space as a flat surface.
Holtzman even assigned fractals to the digital world, recognizing the fractal geometry as a natural geometry for cyberspace, as well as the main factor that should determine the aesthetics of cyberspace. As he says, despite the fact that self-similar structures have been possible before, they could not “exist” without computers, and this, according to him, makes the computer a fractal "device". Fractals are not built on any borrowed metaphor. They belong to the world of computers.
One of the first visions of cyberspace by Gibson: "tunnels of light' in Neuromancer are not built in a curved space time, or fractal dimension. or imaginary tenth dimension, but in the well-known Euclidean geometry.
Benedikt considers the application of certain rules and geometry of the real world as a necessity, which preserves the continuity and smooth transition between the virtual and real and optimal orientation and navigation in the data accessed. On this basis he builds the whole system of rules that should govern cyberspace. These principles are described in his book: Cyberspace First Step - Some Proposals. They are ways for the effective transfer of spatial values of the physical world to cyberspace in order to create a convenient and logical navigation system. Benedikt says:
Ordinary space and time must form the basis of cyberspace. (…) Possible correlations between the behaviors of physical space and cyberspace must be kept. A cyberspace dweller brings expectation of three-dimensional continuity of physical environment in cyberspace, the logic of being in the real space and time. [6]
The aspect of the consistency of the worlds is emphasized by the many creators of VR. If cyberspace is supposed to simulate the 'real', there is no other way than to let it be constructed on the basis of Euclidean geometry. As Benedikt pointed out, the cyberspace user brings to the virtual environment the expectation that the cyberspace should look familiar, be easy and "intuitive" to navigate. But, not all features of this system can be used in the new electronic environment. This is partly because the system of Euclidean geometry in cyberspace is limited to the role of metaphorical representation.
Euclidean geometry also plays an important role in the process of creating new multimedia language, which uses extensively the symbolism it contains. For example, in the symbolism associated with the directions, verticality has always been considered a sacred dimension of space—related to the expression of verticality “over, up, high”—it symbolizes superiority, supremacy and perfection. Not only do directions create symbolic cultural meanings, the geometric shapes are filled with meanings as well, for example, a sphere has always been an ideal form; a straight line is “more perfect” than the curved one; and finally that symmetry is superior to asymmetry.
Bartett House, Second Life
2.2.1. The function of Euclidean geometry in cyberspace
Euclidean geometry is implemented into the cyberspace environment mainly because of its convenience, but also because the laws governing Euclidean systems are well known and have been present in a culture for centuries, and because the world of visual symbols that creates communication platforms belongs to the world created on the principles of Euclidean geometry. However, in electronic environments, Euclidean geometry loses its measurement, descriptive and positioning values. It is not useful in the understanding of mathematical structures, but as a tool that describes and provides guidance.
There is no scale in cyberspace, so the concept of dimension in the mathematical sense does not exist. There is also no objective reference point with respect to which this concept could be built. The territories where the objects could be situated are not specified. Moreover, one place in cyberspace (in the physical sense) can be occupied by more than one object. Cyberspace does not generate any specific “mass”; it is more of a collection of “events”. Properties of cyberspace cannot be described by the Euclidean system, so from the mathematical point of view Euclidean geometry is useless for the purpose of describing it.
Euclidean geometry in cyberspace serves as a metaphor in the way it is described by Rawers: elements and principles are understood as an aesthetic expression of geometric thinking, or as a technical improvement of the temporary memory. They do not meet the descriptive function; they are abstract phenomena—aesthetic tools.
Visualization of forms and their relationships give the basis for data visualization. This is visualization of the use of Euclidean aesthetics, not its mathematical properties. What we call Euclidean geometry in cyberspace is thus a visual representation of the Euclidean geometry—the system of symbols. We see geometric metaphors as more focused on visualizing the symbols than on using mathematical properties of geometry, or as a descriptive and cognitive tool. Instead of Euclidean geometry in cyberspace, we should talk about the aesthetics of Euclidean geometry.
Eyclidean geometry aesthetic in Cyberspace
Asymptote Architecture, New York Stock Exchange (NYSE) VIRTUAL TRADING FLOOR
2.3. Non-Euclidean Geometry in Cyberspace
Euclid in Elements intended to create a coherent mathematical structure based on the geometry of space. Euclid's fifth axiom [7], however, proved to be a weak point of the whole system, which ultimately led to its overthrow.
Attempts to prove the fifth axiom lasted uninterruptedly until the nineteenth century, when mathematicians began to suggest geometric solutions in which the fifth axiom does not exist. German mathematician Carl Friedrich Gauss was the first to develop a revolutionary theory of hyperbolic non-Euclidean space. Eventually, it was published by Bolyai and Lobachevsky. A few decades later another kind of non-Euclidean space was described—an elliptical space.
M. C. Escher, Hand with Refl ecting Sphere, 1935
After rejection of Euclid's fifth axiom (parallel postulate), there are two possibilities left: that a point belonging to the line does not pass any line, or such lines are more than one. Having accepted the first of these possibilities, we obtain an elliptical geometry, if the second, we obtain hyperbolic geometry. In consequence we accept the axiom saying that any two lines intersect at some point, and the concept of parallelism does not exist.
The creation of non-Euclidean geometry had a tremendous impact not only on the perception of the world, but also on the essence of mathematics and geometry. This discovery destroyed the idea that the Euclidean geometry is a faithful representation of physical space. It was this impulse which in effect led to the liberation of mathematics from its function of describing nature. It became obvious that geometry is a human creation, not something that exists in nature. Mathematical spaces came to be seen as abstract logical structures, which also led to the separation of mathematics from physics. All of this started the process of changing the direction of thinking about space and the creation of space. The space began to be perceived as an abstract independent entity.
2.3.1. Elliptical and Hyperbolic Space
The Gaussian breakthrough discovery was the fact that we can perceive the geometry of curved space without referring it to the higher-dimensional Euclidean space, which means that we can perceive an elliptical space (the spherical space), two-dimensionally. Two-dimensional space of a sphere (for example, the image of the Earth's surface) can be considered as an independent space, which operates under the new rules.
On a sphere, the sum of the angles of a triangle is not equal to 180°. The surface of a sphere is not a Euclidean space, but locally the laws of the Euclidean geometry are good approximations. In a small triangle on the face of the earth, the sum of the angles is very nearly 180°.
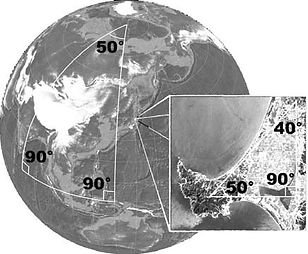
Riemann explains how the sphere can be perceived as two-dimensional elliptic space and proposed a new interpretation of the concepts of point, line and plane. As a plane he chose a surface of the sphere; the points are the positions in the Cartesian style, the position given by a pair of coordinates (longitude and latitude); Riemann’s lines are geodesics of the sphere.
This space was first visualized by Henri Poincaré. Poincaré’s space is not just a model of hyperbolic space; it is a two-dimensional hyperbolic space. In the language of mathematics, this means mathematicians have proven that all possible mathematical descriptions of the hyperbolic plane are isomorphic. If our space is hyperbolic it behaves according to the Poincare model, but in three dimensions.
The invention of hyperbolic space, as an independent space that may exist in the form of two-dimensional visualization, also expanded the concept of space into the abstract realm, closer to the reason than to empirical experience, thus as an abstract space, making it an excellent tool to describe the (abstract) structure of cyberspace.
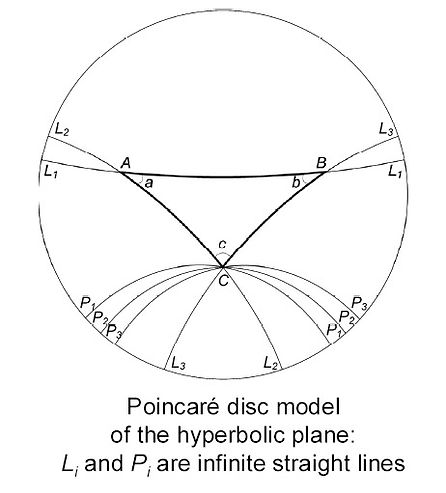
Hyperbolic tesselations
The invention of hyperbolic space, as an independent space that may exist in the form of two-dimensional visualization, also expanded the concept of space into the abstract realm, closer to the reason than to empirical experience, thus as an abstract space, making it an excellent tool to describe the (abstract) structure of cyberspace.
M. C. Escher, Angels and Devils 1960
2.4. Topology in Cyberspace
Topology is the science of transformations, and the science of invariants. [8] Henri Poincaré is the creator of the concept of topology, which was introduced in groundbreaking masterpiece Analysis Situ (meaning 'the analysis of site') in 1895. Topology is the study of the properties of geometric figures that remain invariant even after being subjected to deep deformation, such as the loss of their characteristic metric features: form and dimension. These forms, however, maintain their qualitative properties. Poincaré defined topology as a science that lets us examine the qualitative properties of geometric figures not only in ordinary space but also in space with more than three dimensions.
Figure constructed arbitrarily with deformable material on which neither cutting not welding are possible; there are properties that are conserved when figure so constructed is deformed at will. [9]
Topological deformation of surface
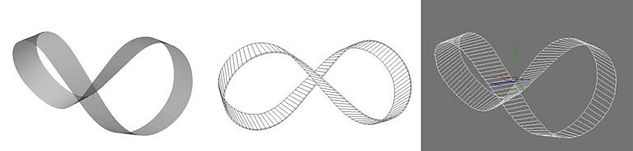
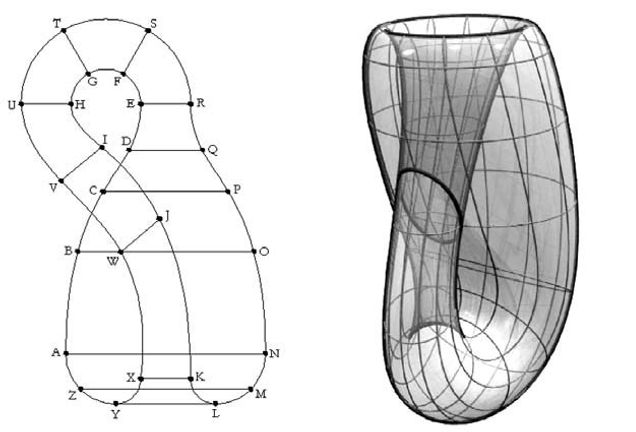
The best-known examples of topological transformations are the Möbius Strip and the Klein Bottle. The theme of the Möbius strip has had a long history before it was defined as a topological space. Since ancient times this theme has appeared in ornamentation as the symbol of infinity (seen in perspective). Möbius strip is a single surface deformed without cuts or tears. It is also has the mathematical property of being non-orientable.
Mobius Strip
A Klein bottle can be formed starting from the Mobius strip, maintaining its properties. The Klein bottle is also a one-sided surface that is enclosed; it has no interior or exterior.
Klein's Bottle
The introduction of topological forms to the language of science and culture resulted in a radical change in the definition of “space”. Instead of a static model, composed of elements, the space started to be perceived as something malleable, variable, and its organization, distribution and allocation have become flexible. Topology has essential meaning for the formation of structures of cyberspace. Every existential space (including cyberspace) is focused around specific action. The first relations ordering these spaces are topological in character. The nature of topology is not based on fixed distances, angles and surfaces, but is based on such relationships as proximity, separation, succession, limitation and continuity. Thus, topology becomes the perfect tool for the formation of cyberspatial substances.
2.4.1 Topology and Architecture
The authors of cyberspatial landscape interpret topology, as well as other advanced mathematical concepts quite freely. The concept of mathematics within the meaning of art, as observed by Michele Emmer, is not mathematics in the strict sense of the term and it would be hard, using these methods, understand the true mathematical ideas. It is rather the configuration of rhythms and the interrelationships of mathematical laws. For this reason, the topology in art (architecture and cyberspace as well) should be considered rather as an example of the geometric metaphor, in the sense postulated by Rawers than as a reliable mathematical tool for the design of electronic spaces.
Giusepa Di Cristina defines the topology in architecture as follows:
Architectural topology means the dynamic variation of form facilitated by computer-based technologies, computer-assisted design and animation software. The topologising of architectural form according to dynamic and complex configurations leads architectural design to a renewed and often spectacular plasticity, in the wake of the baroque and of organic expressionism. [10]
Topology, in its “metaphorical” form, penetrating the architectural grounds, has had a special and profound impact on architecture, radically changing the perception of space. The change mainly concerns the shift from the idea of static understanding of space into a belief in its liquidity and morphology.
Topology in the case of architectural consideration means the study of behavior of surface structures that are subjected to deformation. The surface remembers the spatiotemporal changes in the process of continuous deformation, which gives more opportunities for the architectural distortion of the surface, hence, the form itself. The continuous deformation of a surface can lead to the intersection of external and internal planes in a continuous morphological change. Topology “awakened” architecture to life. The key role in the adaptation of mathematical concepts to topological architecture was performed by computer visualization.
Example of topological aesthetics in architectural design
Zaha Hadid, Thames Gateway
Michel Sanner, Topological surface
2.5. Fractal Geometry in Cyberspace
Fractal geometry is the first geometry, which, although it comes from the need of inventing a more accurate way of description of nature, is considered the most promising system for the construction of structures of cyberspace.
Although fractal geometry was described earlier, the French mathematician Benoit Mandelbrot defined it in the 70s of the twentieth century. At a time when mathematics started to become more abstract and separated from physics and the function of describing nature, Mandelbrot began to consider mathematical problems in terms of shapes, including shapes that correspond to the rules and the forms of nature. Mandelbrot was looking for a simple way to describe the complex nature of objects such as mountains, trees, clouds and coastlines. Traditional geometry, according to Mandelbrot, is not suitable for this purpose:
Why is geometry frequently describes as cold and dry? One reason is its inability to describe the form of a cloud, a mountain, a coast or a tree. Clouds are not spheres, mountains are not cones, coasts are not circles and riverbanks are not regular, not ever light travelers, along a straight line. […] Nature reveals not simply a higher degree of complexity but a completely different level. [11]
Mandelbrot suggested using fractal geometry as a much more appropriate way for describing phenomena occurring in nature. It seems to be 'closer' to these structures. Fractal geometry is a set that has certain characteristics. The main characteristic is the self-similarity.
Like topology, fractal geometry found its way into the popular consciousness, thanks to computer visualization, which allowed to fractals to be “seen”. The electronics visualization of fractals led to the development of software that generates them, therefore, to develop techniques and ways to visualize them and to discover the unique features of these systems for cyberspace. From the “geometry of nature”, fractals have become the geometry of cyberspace.
Mandelbrot Set
2.6.1. Spacetime continuum
Thanks to Einstein’s discoveries a new value—time has been introduced to the geometry. Although time is an important factor in a number of geometric systems (for example the topology of chaotic systems), it was the direct recognition of time as a dimension that once again changed the perception of space.
Modern concepts of geometry also include a time value. As a result, instead of occurrence of points, in spacetime we formulate the term events, that is, points in the four dimensions of space and time. Instead of space ways, we speak of geodesic lines through space and time. Instead of distance, we have a combination of time interval and spatial distance between the events.
Time perceived as dimension is considered to be an important element of the cyberspatial environment. Immaterial cyberspace structures behave as thoughts - they are volatile and they change over time. Cyberspace is alive and its geometry is evolving. Perceiving points as events and replacing the notion of distance (which does not exist in cyberspace), with the concepts associated with time-intervals and the position seems to be a promising direction of research on cyberconstructs.
Various concepts transmitted between the fields, as in the case of the geometric and mathematical concepts discussed here, show that space exists as a cultural category within which there are defined certain structures and rules.
Geometric systems introduce to the processes of creation of space a sense of order. Mathematics and geometry are abstract tools used to organize the abstract space of mind, establishing a hierarchy and building certain structures and rules. However, the geometric systems used to create cyberspatial worlds play completely different roles in cyberspace than in the physical world. Euclidean geometry brings to the cyberspace the systems of symbols and metaphors, which help build existential spaces. It brings the known, allowing the domesticating of new territories. Non-Euclidean geometry showed that space can become an autonomic geometric being, an independent entity existing in numbers, a being created by intellect and remaining close to the reason and stimulating abstract thinking. Non-Euclidean geometry became an independent product and the creative power of speculative abstract mathematical mind. Topology allows perceiving space as a dynamic, fluid, malleable, variable environment, which can be freely shaped and changed in time. The world of fractals is a step towards the discovery of new spaces independent from nature; it is an abstract, mathematical tool for the creation of cyberspatial world. Spacetime has provided us with a new understanding of geometric concepts: points as events, lines as geodesic lines. These concepts are ideally suited for cyberspace which is a dynamic system, based on events.
[1] Norberg – Schulz C., Bycie, przestrzeń i architektura, Murator, Warszawa, 2000, p. 15 (Lynch)
[2] Rawers, P., Space, Geometry and Aesthetics; through Kant and towards Deleuze, New York, 2008, p. 1
[3] Rawers, P., op.cit., p. 3
[4] Emmer M., Mathland, From Flatland to Hypersurfaces, Birkhäuser Basel, 2004, p. 10
[5] Emmer M., op.cit., (Osserman)
[6] Cyberspace, First step, Benedikt M., ed., MIT Press, Cambridge, Massachusetts 1992
[7] If a line segment intersects two straight lines forming two interior angles on the same side that sum to less than two right angles, then the two lines, if extended indefinitely, meet on that side on which the angles sum to less than two right angles.
[8] Emmer M., op.cit., p. 11
[9] Ibidem., p. 66
[10] Ibidem., p. 80 (Giusepa Di Cristina)
[11] Emmer M., op.cit., (Mandelbrot)
[12] Virilio: “One cannot separate the invention of virtual space from fractal geometry. Architect needs to work in fractal dimension.”
[13] Musgrave
[14] Emmer M., op.cit., p. 55
The Sierpinski triangle (also with the original orthography Sierpiński), also called the Sierpinski gasket or the Sierpinski Sieve, is a fractal and attractive fi xed set named after the Polish mathematician Wacław Sierpiński who described it in 1915.
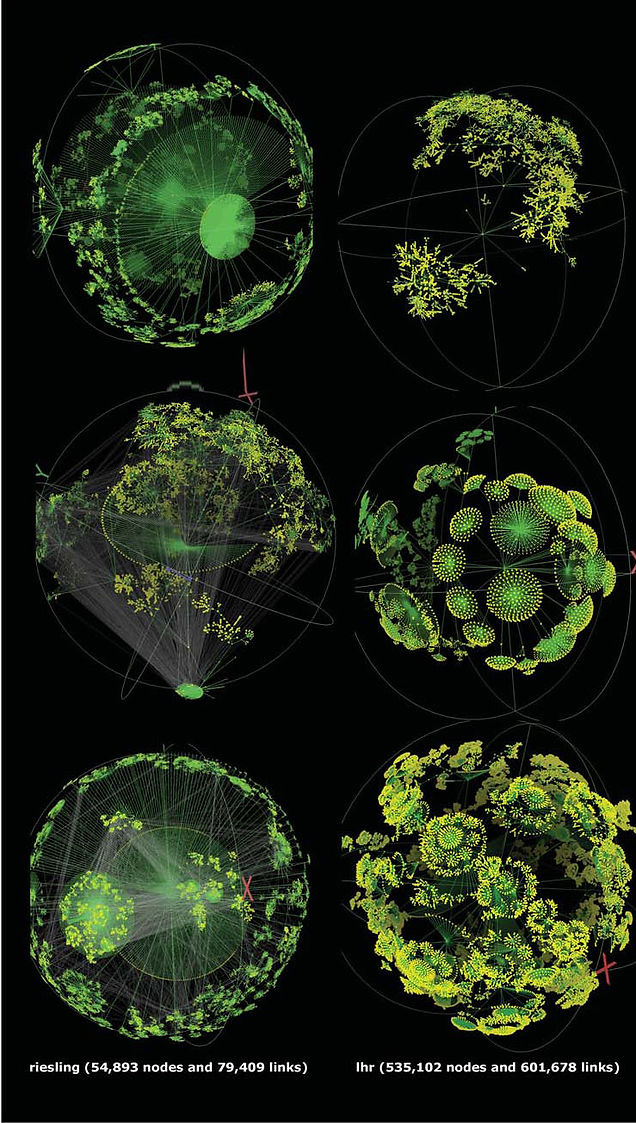
Fractal worlds are visual forms of calculation. Thus, fractals perfectly fit into the specific world of electronic cyber-environment, with no scale and no resolution limits.
2.5.1 Fractals and structure of cyberspace
What role might fractal geometry play in the process of creating the structure of cyberspace? Virillio believes in that crucial role:
You cannot separate the fact of invention of the virtual space from fractal geometry. The architect has to work in fractal dimension. [12]
Kenton Musgrave, Mandelbrot’s student and an expert in computer visualization technologies considers a combination of fractal structure and Euclidean geometry to be an ideal structure of cyberspace. He argues that the fractal geometry allows cyberspace to “grow” inside by adding more detail, which can be noticed by gradual zooming:
Using a fractal representation, you can grow "inward" by adding ever more detail that can be seen by zooming farther and farther in to your cyber construct. [13]
A plot of the Lorenz attractor
This is an excellent feature that allows dealing with the complexity of the cyberspatial construction and also makes possible to visualize one of the basic features of this environment - infinite depth. The beauty of fractal representation, Musgrave says, lies in the fact that compared to the visual effect the model remains very tiny in size.
2.6. Multidimensionality of Cyberspace
Admiration for the concept of multi-dimensionality of space has been present in the science and culture for over a hundred years since non-Euclidean geometry of spacetime was defined by physicists and mathematicians. In the early twentieth century especially the concept of fourth dimension (mainly for the purposes of space) gained on popularity. The fourth spatial dimension was present on cubists, futurists and surrealists’ canvas. It was also a theme for many literary works. For example Howard Hinton, in his 1910, treatise “Fourth Dimension", firmly stated that "the birth, growth, life and death of living organisms is a transitional phase of four-dimensional bodies passing through our space”. The most popular among the publications is Abbott’s Flatland: A Romance of Many Dimensions, the story of a Square, a citizen of “Flatland”, visiting the three-dimensional world. Despite the fact that “Flatland” was already well known in the nineteenth century, and Cubist experiments took over the art world in the early twentieth, multidimensionality, like other mathematical concepts, on a massive scale began to function only after it had been visualized by computer. Emmer said:
It took more than a hundred years for the hypercube dreamed by Square in Flatland to become an object of a mass consumption. [14]
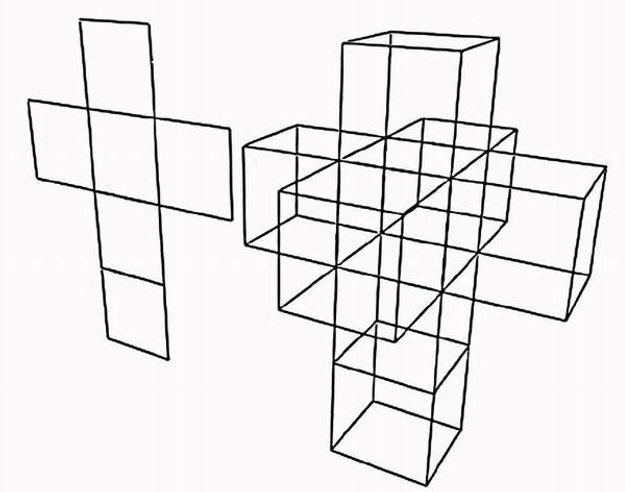
Tesseract
The film Hypercube, which was created in 1979 at Brown University, was the first visualization of the rotating three-dimensional hypercube. In 1984, the same author (Banhoff) and his colleagues visualized hypersphere.
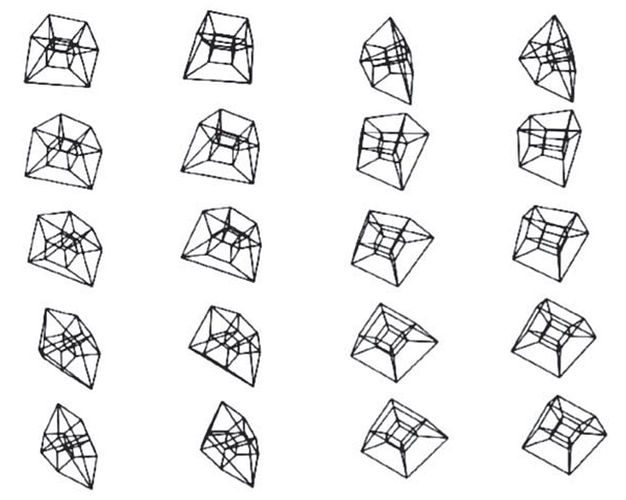
Hypercube rotation
AGNIESZKA SZÓSTAKOWSKA
3. SKETCHES FROM VIRTUAL SPACE - II CYBERSTRUCTURE
1. Abstract
2. Thesis
3. Sketches – Methodology
1.1. Phantomology and Immersion
1.2. The Virtuality and the Myth
2.2. Existential Space
2.3. The Space of the Mind
3.1. What is Cyberspace?
3.1.1. Electricity and Multimedia
3.1.2. Extended sensorium
3.2. Where is cyberspace?
3.2.1. Self-organization (User-Driven Environment)
1.1. The substance of cyberspace
1.2. To sculpt cyberspace
1.2.1. Formation of the interface
1.2.2. Shaping the message
1.3. Structure of cyberspace
1.3.1. The order of space
1.3.2. Spatial coordinates
1.3.3. Right Hemisphere Structures
1.3.4. Lef t Hemisphere Structures
3.1. Examples of cybermetry
3.1.1. Titman’s Zoom Geometry
3.1.2. Leyton’s New Formalism
3.2. An alternative understanding of dimension - a cyberspatial dimension
3.2.1. Metadata
3.2.2. Semantic Dimensions. Semantic Spaces
3.3. Cybermetries without geometry
4. STRUCTURES OF CYBERSPACE
4.1. Kenton Musgrave’s concept
4.2. Michael Benedikt’s concept
1.1. Architectural (r) evolution
1.2. Architectural (re) definition
3.1. Designing the Process
3.1.2. Genome. The processes of nature
3.1.3. The code of cyberspace
3.2. Creating images. The new symbolism of cyberspace
3.2.1. Places
3.3. New design methods. Creating the Worlds
3.3.1. Defamiliarization
3.4. Function and forms of cyberarchitecture
Acknowledgments:
This research project would not have been possible without the kind support of many people. I would like to express my gratitude towards my supervisor, prof. Barbara Borkowska – Larysz and all individuals from the Jan Matejko Academy of Fine Arts in Krakow who helped me with it. My special thanks and appreciations go also to people who helped with the English translation: Charlotte Snyder, Brendan Kennedy and Gus Russo. I am also highly indebted to Edna Emmet and Gus Russo for everything. Many warm thanks go to my wonderful friends for their support: Wiola Mazurek, Robbye and Kevin Apperson, Gail Langstroth, Mark Towles and Sherri Romm Towles. Finally, my deepest thanks go to my family: my parents Ela and Marek and my sister Ania, who encouraged me during the process and especially to my wonderful husband Lucas Lechowski, for his great music and inspiration.
Thank you!
Agnieszka Szóstakowska
CyberEmpathy SPECIAL EDITION 1 / 2011: Sketches from Virtual Reality
AGNIESZKA SZÓSTAKOWSKA
3. SKETCHES FROM VIRTUAL SPACE - II CYBERSTRUCTURE
„Nothing could be more important
than the effort
taken to understand where our
world is going,
and if we should resist, or
whether, accepting the
move, actively participate in it.”
(Stanisław Lem)
Bibliographic description to this article:
3. Sketches from Virtual Space - II Cyberstructure /A. Szóstakowska. CyberEmpathy: Visual Communication and
New Media in Art, Science, Humanities, Design and Technology SPECIAL EDITION 1 /2011.
Cybersky. ISSN 2299-906X. Kokazone.
Mode of access: Internet via World Wide Web
PhD Dissertation 2011
Jan Matejko Academy
of Fine Arts, Krakow
SUBSTANCE OF CYBERSPACE
 CyberEmpathy 9/2014Cyber Art: Piotr Zawojski, Sidey Myoo,Katarzyna Otulakowska, Beata Bigaj-Zwonek, Ika Wato, Juri Czabanowski, Andrzej Głowacki |
|---|
 CyberEmpathy 8/2014Augmented Reality Studies: Fotis Liarokapis, Piotr Zawojski, Elwira Wojtunik, Popesz Csaba Lang, Jarosław Kinal, Mariola Kinal |
 CyberEmpathy 7/2014Visual Strategies: Kseniya Bilychkevskaya, Ika Wato, Juri czabnowski, Elwira Wojtunik, Popesz Csaba Lang, Jan Głowacki, |
 CyberEmpathy 6/2013Code: Juri Czabanozwski, Iurii melnyk, Olha Kvasnytsia, Peter (Basil) Kaminsky, Grażyna Pietruszewska-Kobiela, Andrzej Głowacki |
 CyberEmpathy 5/2013Architecture for Human, Humanism for Architecture: Juri Czabanowski, Barbara Stec, Marika Wata, Katarzyna Kosiniak |
 CyberEmpathy 4/2013Visual Poodle. Contemporary Art in the Public Space: Marika Wata, Hans Peter Hahn, Ruth Loibl, Johann Schuerer, Christa Pawlofsky, Brigit Moller-Klimek, Beata Bigaj, Agata Kus, Michał Hyjek |
 CyberEmpathy 3/2013Soluble Fish in Insoluble Reality: Grazyna Pietruszewska-Kobiela, Andrzej Głowacki, Marika Wata, Piotr Głowacki |
 CyberEmpathy 2/2012Cybersky: Andrzej Głowacki, Piotr Zawojski, Josyp Los, Peter Schmid, Jan Głowacki, Berenika Kowalska, Jarosław Kinal, Katarzyna Krakowiak |
 CyberEmpathy 1/2012Cyber Fields Forever: Andrzej Głowacki, Marian Szewczyk, Piotr Głowacki, Bolesław Jaskuła, Krzysztof Pancerz, Andrzej Głowacki, Marcin Malec |
 CyberEmpathy SPECIAL EDITION 2/2011The Gilliam's Atlas: Jakub Woynarowski, Kuba Mikurda, Michał Oleszczyk, |
 CyberEmpathy SPECIAL EDITION 1/2011Sketches from Virtual Space: Agnieszka Szóstakowska |
There is so much more to check out :
